How much would you bet?
08/09/2012When you want to know how confident someone is, you might ask them "How much would you bet?" This article discusses what it means to be willing to bet X on something.[1]
Let's define the event A as some occurrence which you might bet on. For instance, A might be the event of the Steelers winning a playoff game. We'll refer to P(A) as the perceived chance that A happens.

Rationality
Let's define a rational actor as a decision maker who always chooses the path with the highest expected happiness, or expected utility. In the case of betting, a rational actor will take a bet only if he expects it to leave him in a state of higher utility than refusing the bet. Utility can be expressed as a function of the state of the actor's life; in the real world, these factors may include personal net worth, satisfaction with family life, career, etc. Note that an actor can derive happiness from making others happy, so rational actors aren't always "selfish" in the conventional sense[2].
Our example
For simplicity, let's assume our rational actor derives strictly increasing happiness off of only his own bank balance, P with initial value P0.
Our example will be the following question: "How much would you bet that the result of a fair dice roll is greater than 2?"
Analysis
A is the event of rolling a 3 - 6, and so by elementary statistics
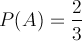
Assume now that the actor was trying to bet some value b such that his expected bank balance is maximized. With some math,
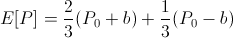
 it follows that the actor's bank balance is maximized when he bets everything! Moreover, we would reach the same conclusion for any event A which has even a 51% of happening.
it follows that the actor's bank balance is maximized when he bets everything! Moreover, we would reach the same conclusion for any event A which has even a 51% of happening.
But most people wouldn't bet their entire bank balance on something as risky as 51% because they are trying to maximize utility, not bank balance.
It's not too hard to see that if utility is positively linear in bank balance,
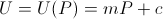

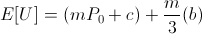
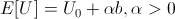
we arrive at the same result of maximizing the amount bet.
Utility functions
Why did maximizing bank balance yield the same result as maximizing utility of a function linear with bank balance? To answer this, first define two utility functions as equivalent if a rational actor following one utility function would always make the same choice as an actor following the other. It turns out that utility functions which are positive linear transformations of each other are equivalent[3].
However, utility functions are generally non-linear in wealth and can result in more interesting solutions.
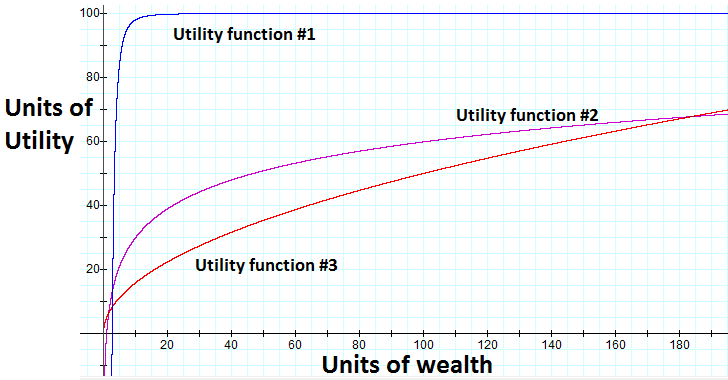
Two properties of common utility functions are that they are strictly increasing in wealth (non-satiability), and that they have diminishing returns over wealth. Formally,

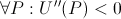
For our basic example, let's take the following utility function (satisfying above properties):
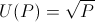
Back to original problem: How much would you bet that the result of a fair dice roll is greater than 2? Let's assume that our rational actor starts with P0 = 100. Let's start by calculating some expected utilities:
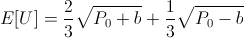


Here we can see that our rational actor under this utility curve would actually refuse a "bet-it-all" on the dice roll as he expects it will leave him in a lesser utility state even though there is a two-thirds chance of winning.
One interesting thing here is that the actor's expected utility is maximized if he bets b = 60[4], but any bet 0 < b < 96 leaves him in a higher utility than no bet at all! So the answer to the question, for this actor with initial wealth 100 and square root utility curve, would be that he's willing to bet up to 96 units but prefers to bet exactly 60 units.
So back to square one. The layman phrase "How much would you bet?" actually could take quite some effort to answer rationally. The methodology, or thinking, used to reason here can be applied to arrive at a variety of conclusions. Try deriving the following truths (ordered in increasing difficulty) on your own:
- 1) In our example above, a wealthier rational actor would have been willing to bet more than 96 units.
- 2) With "common" utility functions, a rational actor wouldn't be willing to bet anything on a 50-50 bet.
- 3) Two utility functions, U0, U1, are equivalent if and only if
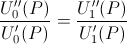
[1] This article is a tip-of-the-iceberg introduction to utility theory. This paper by John Norstad is a very enlightening, easy read I thoroughly enjoyed.
[2] For instance, consider the case where my happiness function is increasing in both my bank balance (with diminishing returns) and my sister's bank balance (with diminishing returns). It's possible that if I strike it rich, it would make me happier to give a chunk of money to my sister rather than keep it; even though this appears to be a selfless choice, this would be the decision of the self-serving rational actor.
[3] Utility theory paper
[4] As an exercise to the reader, find the maximum expected utility by symbolically solving for roots of the first derivative of the utility expectation function with respect to the bet amount.
