Naive graph-based Freecell solving
07/13/2014One of the Windows-pre-installed games my grandfather plays is Freecell. He's become quite good, but every once in a while he'll dare me to get him out of a particularly stubborn position. I began thinking of ways to- algorithmically solve a Freecell board and reading what others have done on the matter and wrote a Freecell solving app. Nothing was particularly complicated, but I thought it touched upon a few interesting topics and was worth sharing. In this article I'll discuss some of the techniques used to put this together.
Before boring you with the details, however, here's a link for you to play around with the solver.
Freecell Solving as Graph Traversal
Where to even begin when trying to code up an algorithm to solve FreeCell? Unlike checkmating an opponent when you have two rooks and king and he only has a king, we can't simply follow a set of rules which will eventually get us to the solution state (whether it be checkmate or moving all of the cards in the foundation cells). Instead, the best I could think of is coming up with a brute-force search of the universe of possible moves.
Imagine we modeled each valid Freecell position as a node, with two nodes being connected if we can move from one to another. This would give us a directed, possibly cyclic, graph. There is only one "completed" node - the one where all of cards have been cleared into the foundation. Representing the problem in this form, we can use any of our favorite graph traversal algorithms to find the solution. Tada!
Pruning and intelligent search
Not so fast - let's do a quick sanity check on the viability of a brute force approach. Let's say there about 8 moves per position (each of the 8 starting columns can move to a Freecell), and say that doing more than 109 operations will take too long. That only gives us log8(109) < 10 moves of depth to search before we run out of operations! If you've ever played Freecell, you'd probably agree that you can't solve many games with 10 moves - for starters there are 52 cards to clear. So it seems though we can't just use a breadth-first-into-oblivion-search or we'd run out of CPU cycles before we found the solution.
Perhaps, however, we could intelligently search only a subset of the graph and still get to the "completed" node. Before we go down that path, it's important to understand that by using heuristics to limit our search space, we are losing our guarantee on finding the shortest solution. Only if our tree was structured better could we find the shortest solution quickly (in polytime) without doing a full BFS-like search. Let's dig into this a bit more. Imagine we're given a constant-time oracle which produces exactly the minimum number of moves to solve the board from any Freecell position - but not the actual solution. Let's call the length of that minimal solution, L. Can you come up with an algorithm to find that minimal solution in polynomial time with respect to L? If you must, the answer is in the footnote.[1]
Unfortunately, I don't know of such a real-life constant time oracle. However, we can use human intuition to build something similar which would give you roughly the number of moves to solve the board from a given position. In fact, the oracle doesn't even need to give you a meaningful number (such as the number of moves required to solve the board) - it can just give you a numeric value monotically increasing (or decreasing) in how good of a position the board is (where a "good" position is one that is close to being solved), and our solver will still find the completed node. This is where we get a chance to put in our "strategies" which will help guide the pruned search to a reasonably short solution.
You can engineer the solver to follow your strategies by having the oracle reward certain pattern and punish others. For instance, we might want the higher ranked cards to be further up in a column, and the 2s, 3s, and 4s to be lower down in a column. We can build the oracle so that it Here are a couple basic strategies that we can hard-code into our solver.
- The more the vacant freecells and vacant columns, the better
- Lower ranked cards are better in the bottom, higher at the top
- The fewer cards remaining in the columns and freecells, the better
Imperfections of a heuristic-based oracle
One problem with an imperfect oracle is that it can lead you uncorrectably astray! Imagine using the algorithm from footnote [1] where at each point you greedily travel to the node with the best oracle score until you've solved the game. With a perfect oracle, the score can never increase from node to another, by construction; there can be no cycles in your solution. At worst, if there is no solution, the score will stay the same and you can therefore detect that there is no solution. However, with an imperfect oracle, the oracle might wrongly suggest you go down one path only to bring you back to where you started - causing an unbreakable cycle. The good news, however, is if you breadth-first-search a few steps in advance and then choose the highest scoring node, as opposed to just choosing the highest scoring immediate neighbor, you can sometimes get over the "humps" caused by a suboptimal oracle. Here is an illustration:
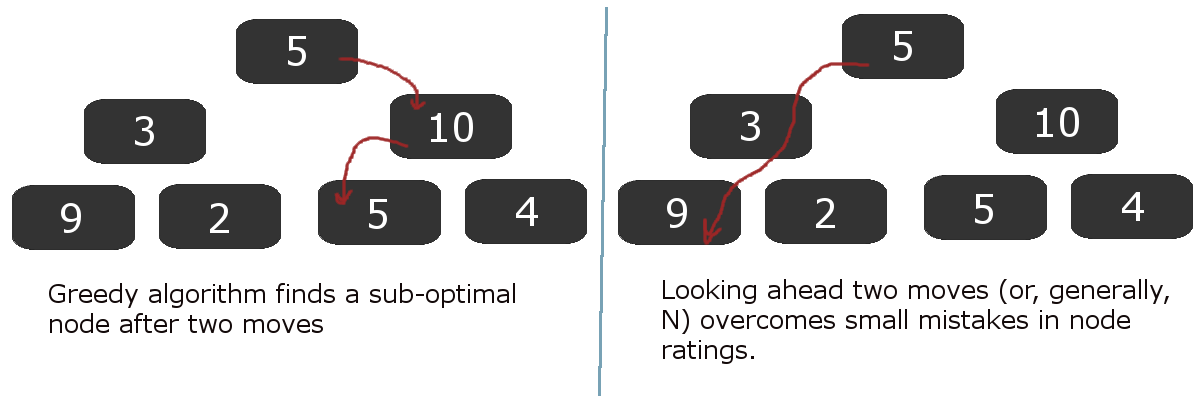
In the diagram above, it should be clear that our heuristic from a node to a "ranking" is a bit flawed - this is what led the greedy algorithm astray. However, real-life Freecell board evaluation algorithms won't be perfect, so tricks like looking ahead a few moves and then choosing the "best" node are helpful. Once you've selected the best leaf node, you only have to remember the path you took to get there. You can forget all the other nodes in the tree and use that memory for further computation.
Move suggestion
Unfortunately even after spending a bit of time on the node evaluation, or "ranking," method my solver would take unusably long to find a solution. I had to come up with another trick. If you're familiar with the rules of Freecell you know that, in the simplest form of the game, you cannot move stacks of cards around between columns. Each turn you can move exactly one card from the columns / freecells to either another column, freecell, or cleared cards. However, some of the Freecell games allow you to move stacks of cards at a time.
It turns out that you can simulate moving a stack of cards at once by a systematic moving of single cards. For instance,
imagine if you had no available free columns, but two available free cells. You can move a stack of up to 3 cards as follows:
So how does this help our solver? It turns out that suggesting "stack moves" as move options (edges in the graph) helps find the solution more quickly because the computer doesn't have to guess all of the single-card moves needed to move a stack, which saves a lot of computation.
As an exercise to the reader, try to prove by induction that you can always move
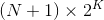cards into a non-empty column, if there are N free cells and K free columns.
Conclusion
Although I don't know of any polynomial-time deterministic freecell solving algorithms, you can use heuristics, move suggestion optimizations, and brute-force search to solve most free cell games. Check out FreeSolved for a free online implementation of the strategies I discussed here. Happy solving.
[1] At each step, evaluate all possible "connected nodes," or neighbors. These represent any possible which can you legally travel to. Choose to move to a node where the "evaluation score" of that node is exactly one less than the current evaluation score. By induction, there must exist at least one such node (if there wasn't a node with score N - 1 neighboring me, then how can I have score N?
