Growth Rate, Log Utility, and Kelly Bets
12/06/2012There's a rigged coin with 60% chance of showing heads. You can bet, with 1-1 payout, on heads. You have an initial bank-roll of P. On any given "turn" you can only bet up to the amount of money you currently have. How should you bet over T turns?
This article uses this problem to show that maximizing the asymptotic growth rate and maximizing log utility both result in Kelly betting. It's also true, under asymptotic conditions, that Kelly bets maximize the median fortune of the bettor.[1]
Maximizing expected value
The first thought that comes to mind is to maximize EV of my bankroll over the T turns. If T = 1, EV is maximized by betting the whole bankroll (analysis). Because the coin flips are IID, my decision on each coin flip is unaffected by the past; I should bet the entire bankroll every time!
This strategy does maximize expected bankroll, but most people wouldn't "bet the house" every time because, in all likelihood, you'll be broke after some time.
Maximizing expected utility
As some betting theory suggests, we should be maximizing expected utility, not expected value. In 1738 Daniel Bernoulli
wrote a paper speculating that the marginal utility of money is inversely proportional to the recipient's net worth[2]. In other words,
if a small unit of money brings you the additional happiness of X, then someone who is half as wealthy as you would receive 2X additional happiness from that same sum of money. Mathematically,
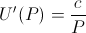 Manipulating this slightly, we see that this is equivalent to the common log-utility function[2]:
Manipulating this slightly, we see that this is equivalent to the common log-utility function[2]:

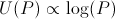
Let's use this utility function to determine how much should be bet on one turn. Without loss of generality, assume we have one unit of money.
We are trying to find the optimal bet 0 < b < 1 on this utility function:
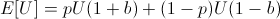
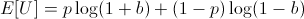
In order to find the b which maximizes E[U], find roots of its first derivative while the second derivative is negative.
Finding a root of the first derivative:
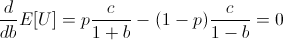
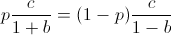
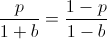

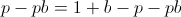
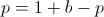
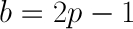
Ensuring that the second derivative is negative there:
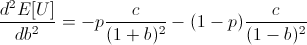
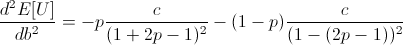
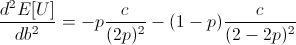

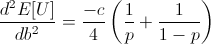 Note that c is the constant from taking the derivative of log(1 + b), and so c is positive.
Thus the entire expression is negative, meaning our root at b = 2p - 1 is a local maximum.
Note that c is the constant from taking the derivative of log(1 + b), and so c is positive.
Thus the entire expression is negative, meaning our root at b = 2p - 1 is a local maximum.
Recall that this calculation only solves the "how much should be bet on one turn?" question. Fortunately, because these gambles are IID, we can apply the same result to all subsequent turns, and conclude that for each turn you should bet a fraction of your wealth equivalent to 2p - 1 at each turn. So, to answer our original question if we have a coin with 60% chance of flipping heads, we should bet 20% of our wealth, on heads, every flip.
Maximizing growth rate
Instead of utility, if we maximize the asymptotic rate of asset growth, we arrive at the same result! Formally,
the asymptotic growth rate is defined as
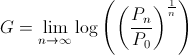
where Pn is the wealth "at time n."[3] In our example, P0 is 1. Now assume that
the bettor is betting some fraction b of his wealth every turn. We can exactly calculate Pn as
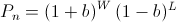
where the bettor wins W times and loses L times. Note that the order of the wins and losses doesn't matter. Simplifying G, we get
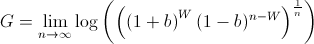
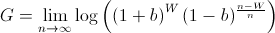
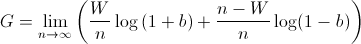
We know that, over time, the bettor will win p amount of the time. Using this, we now must maximize

This is what we want to maximize. But wait a second, this looks an awful lot like the EU of an actor with log utility which we just calculated! In fact, it is!
So maximizing the asymptotic growth rate will have the same result as maximizing EU of a single flip with a log utility function. Thus, if we go through
the math again, we will once again arrive at the conclusion
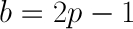
To further nail in the point, let's consider a different approach. Rewind back to
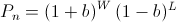
This is the exact, non-asymptotic amount (not utility) which the bettor will have at the end of W wins and L losses. Let's maximize
this instead using conventional calculus (find root of derivative).
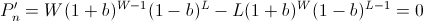
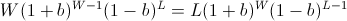
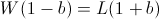


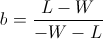
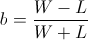
Recall that so far we have not made any asymptotic approximations; the value b described above will always have the highest end balance after W
wins and L losses. As a side note, a negative b value would symbolize taking "the other side of the bet" for the amount abs(b). In order to make further progress, let's now assume that our coin has probability p of flipping heads and the number of trials, n
tends to infinity. We once again have
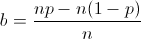
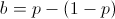
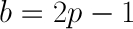
Maximizing median value
One strategy, which remains largely undiscussed, is to maximize your median wealth value over an indefinitely large sample size. Although I won't go into the math, it also holds that betting 2p - 1 fraction of your bankroll, at all betting turns, maximized the bettor's median fortune over the long run[1].Conclusion
In our simple coin flipping game, both maximizing log utility and asymptotic growth rate yield a betting strategy of betting a fraction of your wealth equal to 2p - 1 on each turn. This result is also achieved by using the Kelly Criterion coined by Kelly in the mid 20th century. The criterion can be expanded and re-calculated whenever the game has payouts other than 1:1, but the essense of the results can be explained in as simple a game as the coin flipping used here. If you're interested in the topic, a few good reads can be found in the footnotes, and in a description of Proebsting's paradox, which surfaces weaknesses of this betting style.[1] This article is meant to be a tip of the iceburg introduction into Kelly betting, but a proof of the median claim can be found here. (S.N. Ethier. 2004).
[2,3] Page two of this paper (MacLean, Thorp, Zhao, Ziemba. 2011).
One last source used was this paper (Stutzer. 2010).
