Equity Vesting
10/29/2012Some employers pay employees equity [1] in the company as part of their compensation. And just like how you don't get your entire annual salary in the first pay check, you don't receive all of your equity on the first day. This article does some analysis on the equity vesting process.
Employees
We'll simplify our analysis and assume that employees are rational actors with common utility curves that get value only out of money. In short, this means that employees always prefer more money to less money, and receive strictly decreasing marginal happiness on each additional dollar as they get richer.
We'll also assume that our employee is looking to maximize utility for some arbitrary time, pick two years from now[2]. In the meanwhile employees are free to move around companies at their will.
Companies
Assume companies pay employees in salary and equity. The value of paid salary in two years has low variance, but the value of equity two years from now is less predictable especially for unestablished companies.
Companies give employees equity in the company according to a vesting schedule. A simple linear equity vest gives the employee equity linearly proportional to the amount of time they've worked at the company until they've vested all of their equity. For example if an employee is granted 20 equity units over 4 years with a linear vest, he gets 5 units after the first year, 10 after the second, etc. until the end of the fourth year at which point he recieves no more equity.
Startup Example
Let's consider our employee Bob who wants to work at a startup company. He has a common utility curve, such as
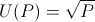
Bob has two years to maximize his expected utility. Let's simplify the world and assume the only options Bob has during this time are to work at either Startup A or Startup B.
Both startups give equity that vests linearly over 2 years and have an independent 5% chance of "making it,"[3] and a majority chance of sizzling out with worthless equity. The equity values in the table below, in the same units as salary, are assuming the company "makes it."
| Equity earned after t years | Salary earned after t years | |
|---|---|---|
| Startup A | 1000t units | 5t units |
| Startup B | 900t units | 4t units |
Let t be the time, in years, Bob spends working for Startup A; (2-t) is the time he works for Startup B. From the looks of it, Bob should work for Startup A for all two years. The only two options are A and B, and he should never be working for the latter because A seems more lucrative. Right? Let's see.
| Who makes it? | Chance | Monetary value | Simplified payout |
|---|---|---|---|
| A, B | 0.25% | t(1000+5)+(2-t)(900+4) | 101t+1808 |
| A | 4.75% | t(1000+5)+(2-t)(0+4) | 1001t+8 |
| B | 4.75% | t(0+5)+(2-t)(900+4) | -899t+1808 |
| Neither | 90.25% | t(0+5)+(2-t)(0+4) | t+8 |
Let's do some expected utility math. Recall that t is the time Bob works for Startup A. Bob expects his utility to be
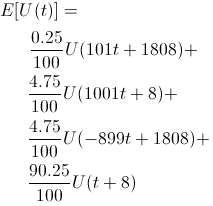
This turns into a simple optimization problem, trying to maximize the above expected utility where
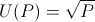
After doing some math (finding roots of derivative of expected utility), we see that expected utility is highest where
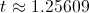
In English, this means that Bob should leave the more seemingly lucrative Startup A for a worse opportunity around 15 months into the job.
What may be even more surprising is the following Wolfram Alpha chart with expected utility on the Y Axis and time spent working for Startup A, in years, on the X Axis:
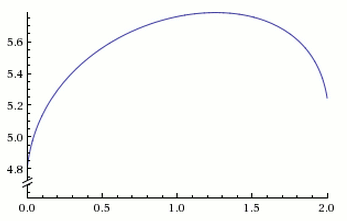
Above we can see that leaving the "better job" after 6, 12, or 18 months are all better options than staying for two years!
The problem with linear vesting
Woah! The payout schedules (under all of these assumptions) actually encourage a rational actor with a common utility curve to leave for a "worse" startup!
This dilemma is the reason why, more simply put, most people prefer a 2% chance shot at $1 million rather than a 1% shot at $2 million. This encourages jumping ships.
The odd thing here is that startup companies often choose a vesting schedule (such as a linear) that causes this dilemma, when they really want the employee to stay for longer!
Mitigating this effect
First off, because of all the assumptions made, our analysis isn't a great correlation to the real world. Nonetheless, the fundamental idea that common utility curves imply risk-averse "hedging" behaviour is something that we have to learn to deal with in compensation packages.
Cliffs
A popular way to mitigate this effect is to impose a cliff on the equity vesting. A linear vest of w equity units over period T with no cliff (of an employee that's worked for t time) has
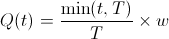
In English, this means that your ownership of the company increases linearly with time until you you've worked for T time at which point you've received all of your equity. A cliff up until time c means that should you work for less than c time units, you receive no equity. So,
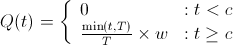
Cliffs discourage employees from leaving before the cliff period, but don't solve the underlying asymmetry between payout and utility. If both Startup A and B had imposed a 1 year cliff, Bob would've still worked for Startup A for about 15 months and left to work for Startup B!
Non-linear vesting
Let t be the time the employee has worked for a company. Our linear vesting schedules can be expressed as

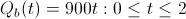
Instead consider the following vesting schedules, which promise the exact same amount of equity after 2 years:
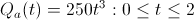

Instead if we re-calculate Bob's optimal moves, we'll see that he should (this time around), work for Startup A for the entire two years. This is because the payout schedule is slower than his utility curve is conservative; Bob doesn't start earning any real equity unless he hangs around which more than accounts for his desire to hedge his bets by jumping ships.
In real life, higher order polynomial equity vesting schedules may be too "complicated", so a more practical solution is delayed additional grants. Assume that startups A and B instead offered Bob one third as much equity in his initial grant, but then gave him two additional equity grants one year apart after he joined. All equity grants vest over two years, with the first one cliffed. His payout would like

This payout, just like higher order polynomial schedules, maintains the desirable positive second derivative in the beginning which helps mitigate risk aversion.
Conclusion
Unestablished companies generally are subject to having a high variance on equity worth. The linear equity vesting schedule, even with a cliff, may not be the best from a rational perspective.
[1] For the purposes of this article, equity can be anything which rises in monetary value as the company does, like shares (linear value correlation) or options.
[2] This isn't a great approximation but will suffice for the analysis. It might make more sense to assume employees are maximizing the overall utility over time with various weights given to different times. Specifically, employees are looking to optimize:
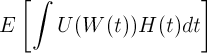
where U(w) is the utility for a given wealth, W(t) is the wealth at time t, and H(t) is how much the actor weights happiness at that point in time. For an actor who is optimizing to have a great time in his 30s, H(t) may look like
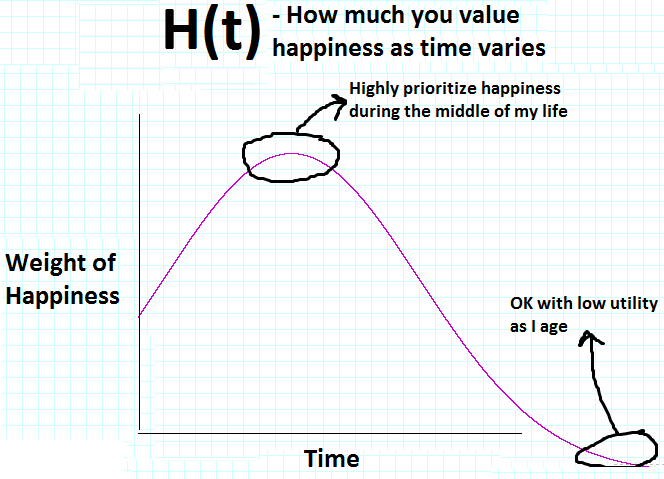
[3] I actually believe the entire world is predictable, but since I can't even tell you what I'm going to have for lunch tomorrow, let alone what companies are going to be worth, I'll fall back on random modeling.
